You are the person who will use this table. ― 2022/01/09 19:28
【この表を使うのはあなたです】
1年半ぶりに中央競馬会のWIN5(指定5レースの全1着を当てる)の分析をやってみた。
2018/1/6から2021/12/26までの218回のWIN5の各レース勝馬の単勝人気は写真のとおりでした。
この表からわかるように、各レースとも1着馬は1番人気馬から5番人気馬までで80%を占めるため、この範囲の馬を選択すれば概ね間違いはないといえる。しかしながら、5レースでは 5×5×5×5×5=3125通りの組合せがあり、1票2票買う程度のチャレンジャーではなかなか的中は難しい。とはいっても80%の確率で1/3125だからいわゆる宝くじほどの低確率ではない。ちなみに年末ジャンボ宝くじの1等当選確率は2千万分の1です。
下の写真は今日のWIN5の結果です。1番人気馬と4番人気馬の組合せでした。想定の範囲内ですね。
確率統計的にWIN5の的中確度を高める情報を得るため二項分布を使って計算した。
以下の写真のとおりです。
この表をどう利用するかはここでは書かない。
本日のウォーキング:0歩
本日のカクテル:前割焼酎
The choice is yours. ― 2020/11/17 10:47
【選ぶのはあなたです】
TEDトークでいい話を聞きました。
TEDサイトによる紹介文は以下の通りです。
『心理学者のバリー・シュワルツは、「偶然」は人生の中で、我々が進んで認めようとするよりもはるかに大きな役割を果たしていると言います。もちろん、たくさん努力して規則を守れば成功する可能性はあります。
しかし、詰まるところ、その他の要素は単なる幸運ということになるでしょう。シュワルツが、運と能力と成功の間にある、見落とされた因果関係について考察し、大学入試についての提言をはじめとする、機会を平等にするための興味深い解決策を提示します。』
そだね、人生は偶然の連続です。そして不思議とうまくいくのです。
この写真は0から9までの数字を書いたチップです。桜の枝から作りました。
これを適当な瓶の中に入れてかき混ぜてから、ひとつ取り出します。
4回繰り返すと4桁の数字ができます。
いまやってみたら「6279」でした。
これで宝くじの”ナンバーズ4”を買います。
幸運がきますように・・・
この「決断!桜チップス」の制作注文受付けます。ただし友人知人のみ。
本日のウォーキング:3910歩
本日のカクテル:不飲※11/18追記:11/17のナンバーズ4第5567回くじの結果は「2304」でした。残念でした。運気向上を待ちましょう!
I understand why. ― 2020/08/08 12:38
【そりゃあ、そうだろうな】
ベンフォードの法則を知ってたらなにか役に立つことがありそうです。
ベンフォードの法則を再掲すると以下のとおりです。
「何らかの数の集まりがあるとする。例えば不動産の価格、各国のGDP、ネットオークションの落札価格、なんでもいいからすべて集める。最初の桁の数字以外を取り去る。するとある法則に適合する。1が2よりも多い、2が3よりも多い。3は4よりも多い。以下同じ。わずかな差ではない。決まった差だ。全体の30%を1が占める。9は5%未満だ。グラフはきれいな曲線になる」
どんな数の集まりでもベンフォードの法則は成り立つのか?
そんなことはないだろうなと思ったので宝くじのナンバーズ3とナンバーズ4の抽選番号の集合にベンフォードの法則を適用してみた。
偏りがあると嫌な数字だよね、ほぼ同じ割合になるんじゃないか?
調査したのは、2014/10/22の第4001回から2016/9/27の第4500回までの500回です。
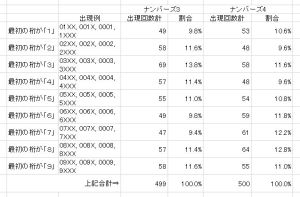
集計結果は以下のとおりです。
最初の桁が「1」から最初の桁が「9」までほぼ同じ割合(約1/9=11.11%)ですね。
ナンバーズの抽選方法はしらないけれど、0から9までの10個の数字の出現確率が同じになるように作ってるだろな(上表では0は集計していないので1/9)。
つまりは、ベンフォードの法則に適合しない数字の集合は誰かが意図的に作り出した数字の集合だということかな。ベンフォードの法則の利用方法が見えてきますね。
※:ナンバーズ3の上記調査期間中に抽せん数字が「000」となった場合が1回あった。ベンフォードの法則では全部0の数はカウントしないみたいなので捨てた。
本日のウォーキング:3375歩
本日のミョウガ収穫数:0本(累積17本)
Benford's Law ― 2020/08/06 09:59
【ベンフォードの法則】
昨夜、ネットフリックス・オリジナル番組、「ビックデータ黄金時代:世界のつながりを科学する」のシーズン1:エピソード4、『桁と数字の法則』を見て、ベンフォードの法則を知りました。
ベンフォードの法則はウィキペディアにも説明があった。
数式は難しくてわけが分からないが、ネットフリックスの解説によれば以下のようなものらしい。
「何らかの数の集まりがあるとする。例えば不動産の価格、各国のGDP、ネットオークションの落札価格、なんでもいいからすべて集める。最初の桁の数字以外を取り去る。するとある法則に適合する。1が2よりも多い、2が3よりも多い。3は4よりも多い。以下同じ。わずかな差ではない。決まった差だ。全体の30%を1が占める。9は5%未満だ。グラフはきれいな曲線になる」
宇宙は不思議に満ちている。
日本中央競馬会(JRA)のWIN5(5重単勝式馬券)の的中番号で確認してみた。
元データは2018/1/6から2020/8/2までのWIN5投票で、143回715レースの結果です。
このデータにベンフォードの法則を適用した結果は以下のとおりです。
不思議だ、ベンフォードの法則に適合してますね。
さらに標本数を増やしていくと、ベンフォードの法則でいう割合にさらに近づいてゆくんだろうな。
ということは、
これからのWIN5では、「1」番人気馬への投票を抑え気味にして、「8」番人気馬や「9」番人気馬へ投票するのがいいんでないかい。
本日のウォーキング:72歩
本日のミョウガ収穫数:3本(累積17本)
It's over between us. ― 2020/07/26 17:20
【私とJRAとの関係は今日で終わりました】
今日、中央競馬で発売の”WIN5”の投票数はすごかった。
なんと、3381万3341票でした。
通常は650万票くらいですから5倍以上ですね。
理由は先週のWIN5で的中票がなくキャリーオーバーが4億6千万円もあったからですね。
WIN5でキャリーオーバーは年に1回あるかないかです。
払戻金額は発売金額の70%だというから、今日の払戻原資を計算すると、
発売金額は33億8133万4100円だけれど、4レース目に出走取消があったからその分は返還しなくちゃいけないから実売上は31億5734万3800円ですね。
結果は下図の通りでした。
払戻金総額は、
31億5734万3800円×0.7+4億6409万1040円(キャリーオーバー分)=26億7423万1700円
的中票数は3274票だから、
払戻金は一人当たり81万6808円になります。
そうか、8円は切り捨てられたのか。
・・・・・
私も通常なら1票買うところを今日は4票も買いました。
結果は無残でした。
赤丸は的中したレースです。なんの意味もないけどね。
本日のウォーキング:40歩
The horror game you're playing is very scary. ― 2020/05/31 18:41
【君のやっているホラーゲームはとても怖いね】<-英会話の練習文です。本文とは関係ありません。
今日は第87回日本ダービーの日でした。
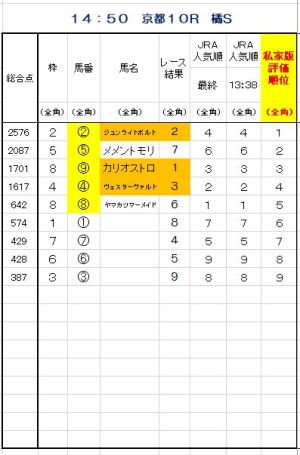
私の評価式による順位(以下、H順といいます)とJRAの人気順(以下、N順といいます)、およびレース結果は以下のとおりでした。
H順位もN順位もほとんど差がなく、前評判通りの馬に投票して的中してもおいしくない。もちろん、私のような少額投票者にとってはという意味です。
今回の場合、私の流儀でH順1位から3位までの馬連3頭ボックス買いした場合、⑤番⑫番が的中して、「300円→270円」だった。的中してもマイナス30円。
本来ならば買うべきレースではなかったが、1時間もかけて評価表を作ったので買ってみたくなった(これがいけないところだな)。
私がチャレンジしてみたのは・・・、
あっけなく撃沈。マイナス200円。
次回は6月7日の安田記念です。
※
3着の⑥番ヴェルトライゼンデはN順10位、H順16位でした。多くの人が何かを見落としていたので10位や16位にいたと考えたい。そいつを見つけることができたら予言者の領域に近づくのだが・・・。修行しましょう。
※※
以下は、”本レースでは同一所有者の馬(⑤番⑩番⑬番)が3頭出場した。⑩番⑬番の騎手は⑤番コントレイルが走りやすくなるように操舵したように見える”という記事です。心情としてはありえるな。これからはこういう点も考慮しなくちゃいけないか。
本日のウォーキング:2604歩
I was fired because of my problem with gambling habit. ― 2020/05/10 21:07
【私は賭博癖のために問題おこして会社を首になりました】<-英会話の練習文です、本気にしないでね。
新型コロナウイルスの感染状況がどうなっているのか、データから分析するのに学者がいろいろ苦労しているようです。競馬だって、どの馬が1着になるか分析するのは大変です。
競馬レースの評価式を作って、ここ3カ月ほど実レースの結果でシミュレーションしてきました。なかなかいけそうじゃない!って感じの計算式ができました。
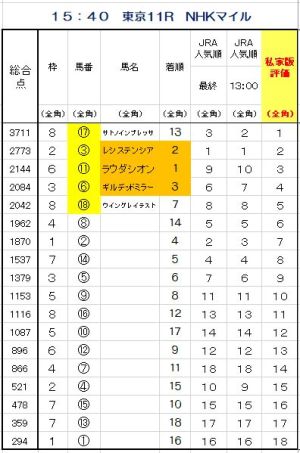
今日のWIN5対象レースとなった5レースについてシミュレーションしてみました。
以下のとおりです。
□1レース目
もし私家版評価(以下、私評)1番から5番までを、
・馬連5頭ボックス買いの場合、1000円→1530円
・3連複5頭ボックス買いの場合、1000円→1540円
・ワイド5頭ボックス買いの場合、1000円→1220円
□2レース目
もし私評1番から5番までを、
・馬連5頭ボックス買いの場合、1000円→1300円
・3連複5頭ボックス買いの場合、1000円→1430円・ワイド5頭ボックス買いの場合、1000円→1220円
□3レース目
もし私評1番から5番までを、
・馬連5頭ボックス買いの場合、1000円→0円
・3連複5頭ボックス買いの場合、1000円→0円・ワイド5頭ボックス買いの場合、1000円→0円
□4レース目
もし私評1番から5番までを、
・馬連5頭ボックス買いの場合、1000円→800円(的中しても収支はマイナスになりました)
・3連複5頭ボックス買いの場合、1000円→590円(的中しても収支はマイナスになりました)・ワイド5頭ボックス買いの場合、1000円→730円(的中しても収支はマイナスになりました)
□5レース目
もし私評1番から5番までを、
・馬連5頭ボックス買いの場合、1000円→4200円
・3連複5頭ボックス買いの場合、1000円→19620円・ワイド5頭ボックス買いの場合、1000円→9040円
【考察】
・ピンポイントで1着馬を見つけることなどできません。できるのは1着候補馬を見つけることだけです。
・1レース目と2レース目は安めに的中したので配当は少なかった。200円や500円の利益に1000円賭けるのはばかげているとも思えるが、それはレース結果を見て言ってるわけで、1レース目の場合、もし高めが的中したら(例えば6番人気の⑤番が3着に入賞したら)馬連②⑤でオッズは45.4倍だった。この馬連5頭ボックス買いには的中したら1530円から4540円までの幅があったわけだけど・・・、この程度の利益に1000円賭けるのはやっぱりだめだな。
・3レース目のように私評順と人気順がバラバラになるパターンの場合には買わないようにすべきだ。
・4レース目は安めに的中したので収支がマイナスになった。もし高めに的中した場合、例えば5番人気の②番が3着入賞時には馬連②⑧で34倍のオッズだった。ボックス買いなので配当に幅がある。どうするかは賭けですね。この場合は買わないという選択が妥当でしょう。確率的には安めに来る可能性の方が高いから。・4レース目のように人気順1位から5位までの5頭ボックス買いはいけない。的中しても利益はマイナスか僅か、外れれば大損です。
・最新の評価式では本4例しかやってない。本来ならば、これから過去のレースについてもシミュレーションすべきだが疲れるのでやらない。手作業で馬データや騎手データを調べながらエクセル表に入力するので1レース分析するのに1時間かかります。疲れますが通常は当日メインレースだけなので手作業のままで問題ないでしょう。
・今日評価したうち、買っていいのは5レース目だけでした。トータルで勝つには如何に買わないかということだな。
来週と再来週のレースについてもシミュレーションするが、この評価式は修正しないでおく。
5月31日の日本ダービーはどうなるでしょうか。
本日のウォーキング:0歩
Amaterasu save me, too! ― 2020/05/03 17:34
【天皇家の守護神さま、我も助けたまえ!】
今日は春の天皇賞でした。
レース結果は、1着1番人気⑭番フィエールマン、2着11番人気⑥番スティッフェリオ、3着4番人気⑤番ミッキースワロー、でした。
私はといえば・・・、
惨敗でした。
私の1番評価となった⑫番がビリケツですから、評価式の見直しが必要ですね。
表を見ればわかるように、今回も”神の評価(レース結果)”と”人間の評価”にはズレがあった。
このズレを最小にする方法または補正する方法を見つければいいのだ。
その方法は感覚的なものやパターン認識的なものであってもいいはずだ。
神のなせるワザがまだ見えない。
疲れた。
次回は5月31日の日本ダービーです。
本日のウォーキング:89歩
I know you'll do a fantastic job. ― 2020/03/29 17:15
【あなたがすばらしい仕事をすることはわかっていますよ】
今日は第50回高松宮記念レースが行われました。
結果は1着⑯番モズスーパーフレア、2着⑧番グランアレグリア、3着③番ダイアトニック、でした。
実際は⑪番クリノガウディが1位入線だったのですが、最後の直線コースでクリノガウディが他の馬に対して進路妨害したということで(騎手の意思じゃなく、馬だから言うこと聞かないんですね)、審議の結果、進路妨害がなかったならばこうなったという順番に決まりました。
解説者たちの事前評価はこんな感じでした。
黄色が投票者の評価、緑色が競馬ファンの評価です。人間の評価はほぼ同じでした。
そして、人間の評価とレース結果はかなりズレています。
賭けが成立する所以ですね。
審判員さんたちはいい仕事をしました。
心強いですね。
ウフフ。
次回は5月3日の第161回天皇賞です。
本日のウォーキング:0歩(自宅引きこもり))





























最近のコメント